Common Subsequence 解説

問題名：Common Subsequence (PKU)
出典：Southeastern Europe 2003
難易度：☆☆☆
問題の種類：DP
解法：LCS (Longest Common Subsequence)
解答ソースコード：
- 1458-deq.cpp

アルゴリズムの概略

DPの四天王（？），LCS (Longest Common Subsequence) そのままの問題です。アジア地区予選など，通常はこれをひねった問題が出てきます。

LCSとは，二つの値の列（この問題では文字列）が与えられて，最長の共通部分列を見つける問題です。部分列は連続している必要はありませんが，順序は変更してはいけません。例えば X = "abcfbc", Y = "abfcab" であればLCSは "abfc" や "abcb" になります。 LCSは一般的に複数ありえますが，この問題ではその長さだけを出力すればいいので，それらのLCSを区別する必要はありません。

アルゴリズムの解説を行いましょう。入力を string a = "abac", b = "abaa" とします。 a, b の部分文字列を a[0..3] = "aba", a[0..0] = "" という風に表し，最長の共通部分列の長さをLCS長と呼ぶことにします。 LCSでは「a[0..y], b[0..x]のLCS長: LCS(y, x)」を求めるのに，

a[0..y-1], b[0..x-1] のLCS長: LCS(y-1, x-1)
a[0..y-1], b[0..x] のLCS長: LCS(y-1, x)
a[0..y], b[0..x-1] のLCS長: LCS(y, x-1)

の3つの最適解を用います。例えば a[0..2] = "ab", b[0..2] = "ab" のLCS長 (LCS(2, 2) = 2) は，

a[0..1] = "a", b[0..1] = "a" のLCS長 (LCS(1, 1) = 1)
a[0..1] = "a", b[0..2] = "ab" のLCS長 (LCS(1, 2) = 1)
a[0..2] = "ab", b[0..1] = "a" のLCS長 (LCS(2, 1) = 1)

から導くことができます。

もし（添え字が1から始まるとして）a[2] = b[2] であれば（この場合はそうですね），a[0..1] と b[0..1] の両方に a[2] (= b[2]) を足したものなのでそのLCS長は1増えるはずです。ですから，LCS(2, 2) = LCS(1, 1) + 1 といえそうです。また，a[0..1] = "a", b[0..2] = "ab" から a[0..2] = "ab" と伸ばせば，つまり LCS(1,2) + 1 が最適解となるケースも考えられそうです。しかし，これは反例が見つかります。LCS(3, 4)のケースがそうです。

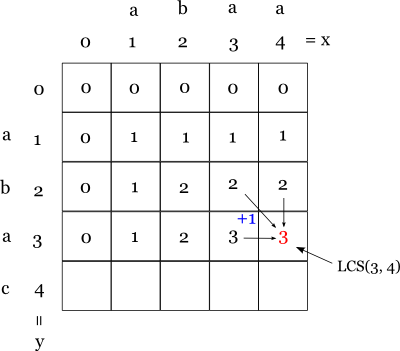
LCS(3, 4) { a[0..3] = "aba", b[0..4] = "abaa" } ですが，これを LCS(3, 3) { a[0..3] = "aba", b[0..3] = "aba" } に1足したものから導いてはいけません。 b[0..3] = "aba" を b[0..4] = "abaa" に伸ばしたからといってマッチする文字列長が増えるわけではありません。

一般的に，図でナナメ右下に行くのは両方の文字列で「次の文字がマッチする」状況（LCS長を +1 する），右や下に行くのはマッチしない状況（LCS長はそのまま）を意味しています。

ですから，LCS(y, x)を求める場合，a[y] = b[x]であれば

LCS(y, x) = max{LCS(y-1, x-1) + 1, LCS(y-1, x), LCS(y, x-1)}, when a[y] = b[x]

で求められます^*1。

それでは a[y] != b[x] の場合はどうなのかというと，この場合は右下に進む場合にマッチしていない（LCS長が 0 しか増えない）ので，

LCS(y, x) = max{LCS(y-1, x-1), LCS(y-1, x), LCS(y, x-1)}, when a[y] != b[x]

で求められます^*2。

なお，当然 LCS(y, 0) = LCS(0, x) = 0 です（a[0..0] = "" という空文字列は共通部分列を持たない）。 LCS長は右もしくは下に行くほど単調増加していくことに注目しましょう。 LCS(a.length, b.length) が求めるLCSの長さになっています。

アルゴリズムの計算量

n = 文字列Xの長さ，m = 文字列Yの長さとすると，求めるテーブルの大きさは (n, m) で各ノードは定数時間で求まる（3つの値のmaxを取るだけ）ので，結局全体の計算は O(n×m) で求まります。

アルゴリズムの実装

この問題はループで解いてもメモ化探索で解いてもそれほどコーディングは変わらないと思いますが，どちらかというとループで解いた方が書きやすく簡単な印象があります。

ループで解く場合，擬似コードは次のようになります（とはいってもほとんどCと同じです）：

for each table[MAX_Y][MAX_X] = 0  // DP表を初期化
for y = [1, a.length]:
  for x = [1, b.length]:
    match = ( a[y-1] == b[x-1] ? 1 : 0 )
    value = max(table[y-1][x-1] + match, table[y-1][x], table[y][x-1])
    table[y][x] = value

printLine t[a.length][b.length]

ところでこの問題，文字列の文字数が問題文に与えられていませんが，適当に 0 < str1len, str2len < 500 と仮定すると問題が解けました。

補足1: これはよく見るともっと簡単に求められます。下図を見てください。

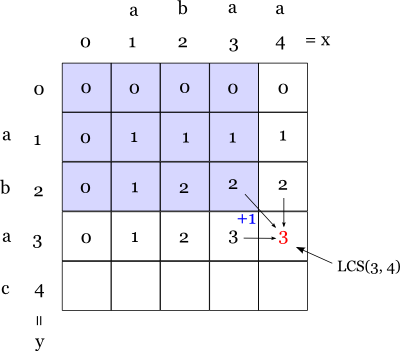
この図において LCS(y-1, x-1) = LCS(2, 3) は青色の領域で最大です。言い換えれば，青色の領域の値のいずれかを v とすると v <= LCS(y-1, x-1) が必ず成り立ちます。ですから，LCS(y-1, x) や LCS(y, x-1) はかならず LCS(y-1, x-1) と同じか 1 大きいだけになります。従って LCS(y-1, x-1) <= LCS(y-1, x), LCS(y, x-1) <= LCS(y-1, x-1) + 1 が成り立つので，

この式は簡略化されて，a[y] = b[x] のときは単に LCS(y, x) = LCS(y-1, x-1) + 1 で求まります。

なぜわざわざ max を取っている式を紹介したかというと，この簡略化は単純なLCSでは成り立ちますがLCSを拡張したアルゴリズム（例えば塩基配列の類似度を求める）では成り立たないからです。一般性もなく，特に計算量的にも大きく変わらないので，この簡略化は忘れてしまってよいと思います。

補足2: この場合も補足1と同様に LCS(y-1, x-1) <= LCS(y-1, x), LCS(y, x-1) <= LCS(y-1, x-1) + 1 が成り立つので，

この式は簡略化されて，a[y] != b[x] のときは LCS(y, x) = max{ LCS(y-1, x), LCS(y, x-1) } で求まります。

$Id: index.shtml 1335 2007-03-01 09:06:39Z SYSTEM $

deq notes