The Secret Number 解説

問題名：The Secret Number (PKU)
出典：Problem C, ACM/ICPC Japan Domestic, 2003-10-03
難易度：☆☆☆
問題の種類：DP
解法：動的計画法
解答ソースコード：
- 2030-deq_loop.cpp（ループ）
- 2030-deq_memo.cpp（メモ化探索）

アルゴリズムの概略と計算量

素直な方法

「2次元のマトリックスから最も大きな数字列を探し出せ」という問題。真っ先に思い浮かぶのは「始点ノードを探して再帰で右or下に数字を連結していく」という解法でしょう。先頭のゼロや細かなあれこれを無視すると，こういう感じのコーディングになります：

def rec(x, y, string):
  string += field[x][y]
  answer = max(answer, string)
  if 右が数字:
    rec(x+1, y, string)
  if 下が数字:
    rec(x, y+1, string)

answer = ""
for x in [0, WIDTH):
  for y in [0, HEIGHT):
    if field[x][y]が数字 and 左が非数字 and 上が非数字:
      rec(x, y, "")

しかし，残念ながらこれではこの問題は解けません。この解法にとって最悪のケースは「入力フィールドが全て数字の場合」で，このとき計算量（組み合わせが何通りあるか）は

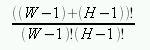
となって，W + H < 70 という条件より W = H = 35 を代入すると 2.8×10¹⁹ となって私たちが生きている間には解けなくなります。

動的計画法

全探索で解けない問題は何らかの枝刈りを行って探索空間を小さくする必要があります（枝刈りだけとは限りませんが，ICPCではたいてい枝刈りです）。この問題では実は「一つ小さな部分問題の最適解を使うと効率的に解ける」という性質があって，そのような性質を利用して解くアルゴリズムは動的計画法 (Dynamic Programming)，略してDPと呼ばれています。ほとんどの場合DPは非常に効率的な枝刈りを行えるので非常に高速です。

さて，DP自体の説明は今のところは省いておいて，実際にDPでこの問題を解くアルゴリズムを説明しましょう。問題文の例題（以下の図）で考えてみます。

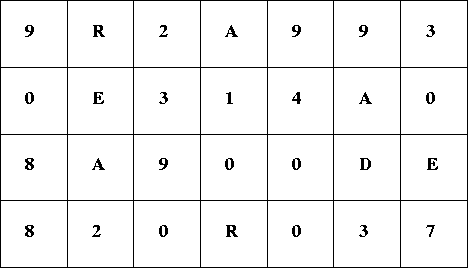
DPでは最初に長さ1 (n = 1) のときの確定解を求めます。ここでは，次の3箇所のノード（赤色）は左にも上にも数字がないのでその場所における解が確定します。

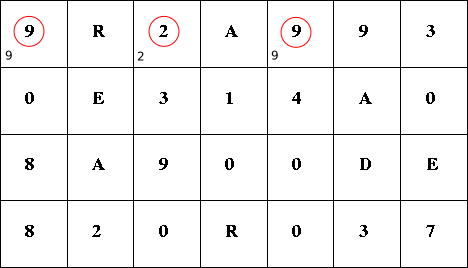
これで「長さ1の場合」の解が求まりました。次は長さ2 (n = 2) の場合に確定できるノードですが，それは次の3箇所（赤色）です。

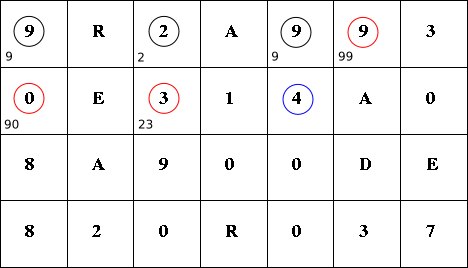
これらの赤色のノードは左のノードも上のノードも状態や値が確定しているので，最適値であることが分かります。青色のノードは，上は確定していますが左が確定していないので，今回は確定させることができません。

同じようにして，n = 3 の確定ノードは次のように求まります。

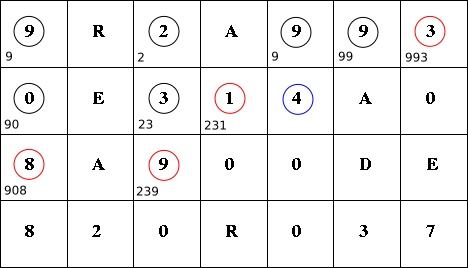
n = 4 の確定ノードは次のようになります。

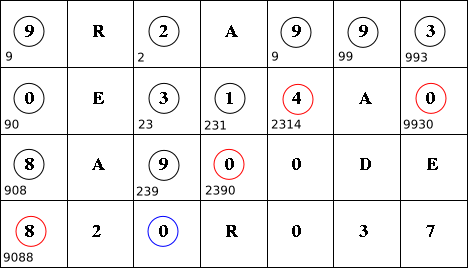
ここで今まで青色だった「4」のノードの値が2314に確定しました。当然94よりも2314の方が大きい数字になるからです。解釈を変えると，最初に挙げた再帰による全探索ではこの94という可能性も下の0のノードに伝播させていたわけですが， DPの方法ではその可能性を枝刈りしている，とも理解できます。

これは n = 70 で必ず終了します（フィールドサイズが W + H <= 70 なので）。もし毎回フィールドを全て走査してチェックしたとしても，計算量はたかだか (W + H)×W×H となって 70×35×35 = 85,750 回程度計算を行えば終了します（後で触れますが実際にはもっと少なくできます）。最初に求めた n! のアルゴリズムとは大きく違いますね。

さて，DPの解法はごくごく普通の考え方であることがお分かりいただけたかと思います。 DPの考え方の「きも」は次の2つしかありません：

あるノードの最適解を確定するのに，一つ前のノード（一つ小さなサイズの問題）の最適解を利用する
一度求めた解を再度計算し直すことはしない（記憶しておく）

まぁ，2つといっても実はこの2つは同じことを別の見方で言い直しただけなのですが。しかし，これら2つの見方はことに重要で，この2つのことがらが同じだと感じれるようになるまでDPの問題をいくつか解いて感覚的にDP解法を身に付けることをおすすめします。

アルゴリズムの実装

ループ解法

上の説明では「n = 1 のとき」，「n = 2 のとき」と見て行きました。しかし，この問題では「右と下にしか連結していかない」，言い換えれば「あるノードにおける解は左と上にしか依存しない」，つまりは「左のノードと上のノードが確定していればそのノードの値も確定する」といえます。ですから，下図のように走査していけば後戻りせずに順々に値を確定していけます。

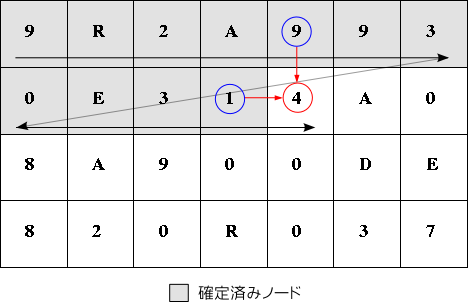
この場合，プログラムは非常に簡潔で

answer = ""
for y in [0, HEIGHT)
  for x in [0, WIDTH)
    if field[y][x] < '0' or '9' < field[y][x]:
      table[y][x] = ""
    else:
      table[y][x] = maxstring(table[y-1][x], table[y][x-1]) + field[y][x]
      answer = maxstring(answer, table[y][x])

で答えが求まります（ただし「添え字の範囲チェック」や「先頭のゼロの排除処理」が必要）。この場合の計算量は明らかに O(W×H) で，ループの内側も文字列の max を取るだけという計算量の少ない単純なものになります。

メモ化探索

実はDPを記述する方法は2種類あって，今まで述べてきたのはループで書いた場合の考え方です。もう一つ，再帰関数で書く場合の考え方があって，メモ化探索あるいはメモイズと呼ばれています。メモ化 (memoize) とは，一度解いた答えはメモっておいて，次にその答えが必要になったらそのメモを読むという意味です。基本となる考え方は上のループの場合で述べたのと一緒ですね。

メモ化探索の場合，冒頭で述べたように再帰関数を書きます。ただし，始点ノードから呼び出してもいいのですが，ループで書いた場合のように答えは終点ノードに集まってくるので，終点ノードを探してそこから再帰関数を呼び出す方が自然と書けます（終点ノードの確定値が欲しい解の候補ですから）。

メモ化探索のコーディングは，まずは普通に全探索の再帰関数を書き上げます。ただし，再帰関数は値を返すように設計します。

def rec(x, y):
  if x < 0 or y < 0 or field[y][x]が非数字:
    return ""
  else:
    return maxstring( rec(x, y-1), rec(x-1, y) ) + field[y][x]

answer = ""
for y in [0, HEIGHT)
  for x in [0, WIDTH)
    if field[y][x]が数字 and 右が非数字 and 下が非数字
      answer = maxstring(answer, rec(x, y))

このプログラムを実装して走らせると，小さな問題セットには正しく答えが出て，大きな問題セットには答えが出ないことが確かめられるはずです。もしそうならないなら，バグがあります。直しましょう。

小さな問題セットに正しく答えが出ることを確認したら，おもむろにプログラムにキャッシュを付け足します。メモ化のことです。メモ化（キャッシュ）は基本的に4行書けば達成されます。すなわち，

キャッシュ変数の宣言
キャッシュの初期化
再帰関数のreturn直前：キャッシュへの代入
再帰関数の始め：キャッシュがあれば返す

です。上の擬似コードに実際に実装してみましょう。

def rec(x, y):
  if x < 0 or y < 0 or field[y][x]が非数字:
    return ""
  else:
    if cache[(x, y)]が存在する:
      return cache[(x, y)]
    cache[(x, y)] = maxstring( rec(x, y-1), rec(x-1, y) ) + field[y][x]
    return cache[(x, y)]

answer = ""
cache = {}
for y in [0, HEIGHT)
  for x in [0, WIDTH)
    if field[y][x]が数字 and 右が非数字 and 下が非数字
      answer = maxstring(answer, rec(x, y))

4行が追加され，1行が変更されました。ただし，もともとのアルゴリズム自体は何も変わっていません。もともとが例外処理を除いた擬似コードなのでけっこう追加されたように感じますが， 50行のC++ソースコードでもメモ化には通常4～5行程度しか要らないので，実際に書いてみると非常に楽な作業です。実際のC++ソースコードは自分で練習で書いてみるか，解答ソースコードを参考にしてみてください（ただし解答は文字列型のメモリ管理をさぼるためにメモ化でいじってる部分が通常よりも多いのですが）。

けっこう長くメモ化探索について説明してきましたが，この問題をDPで解く場合はメモ化探索よりもループで書いた方が素直で簡単です。

$Id: index.shtml 1335 2007-03-01 09:06:39Z SYSTEM $

deq notes