ダイクストラ法（最短経路問題）

ダイクストラ法 (Dijkstra's Algorithm) は最短経路問題を効率的に解くグラフ理論におけるアルゴリズムです。スタートノードからゴールノードまでの最短距離とその経路を求めることができます。

アルゴリズム

以下のグラフを例にダイクストラのアルゴリズムを解説します。円がノード，線がエッジで，sがスタートノード，gがゴールノードを表しています。エッジの近くに書かれている数字はそのエッジを通るのに必要なコスト（たいてい距離または時間）です。ここではエッジに向きが存在しない（＝どちらからでも通れる）無向グラフだとして扱っていますが，ダイクストラ法の場合はそれほど無向グラフと有向グラフを区別して考える必要はありません。

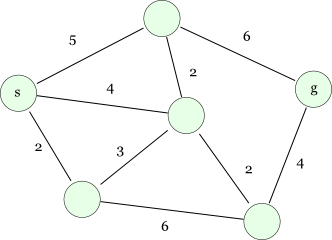
ダイクストラ法はDP（動的計画法）的なアルゴリズムです。つまり，「手近で明らかなことから順次確定していき，その確定した情報をもとにさらに遠くまで確定していく」方法で， DPと同じ精神を持っています。

上の図で明らかに分かることはというと，まずスタートノード自身への最短距離（最小コスト）は 0 です。全く移動しないで済むので，これは明らかに最適解です^*1。そこまでの最短距離が求まったノード（最適解が確定したノード）を次のように赤色で表してみることにしましょう。最短距離はノードの近くに赤色で併記しています。

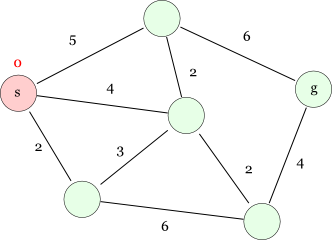
次に，今のところスタートノードだけが確定しているので，そのスタートノードから辿れるところをチェックします。ここでは，スタートノードから辿れる経路は3つ存在し，それぞれの距離は次のように 5, 4, 2 となっています（以降，今のところ判明している最短距離とその経路を青色で示します）。

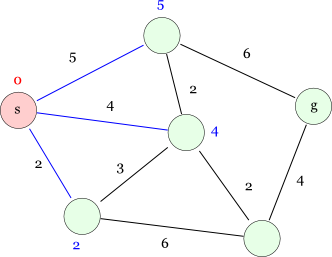
さて，次に明らかなこと（＝確定できそうなノード）を探しましょう。今のところ，未確定ノードへの最短距離は 5, 4, 2 の3つしかありませんから，もし負のコストを持つパスが存在しなければ「左下の距離2のノード」に 2 よりも少ない最短経路が見つかることはありません^*1。従って，「左下の距離2のノード」への最短距離は2で，このノードの最適解を確定させることができます。

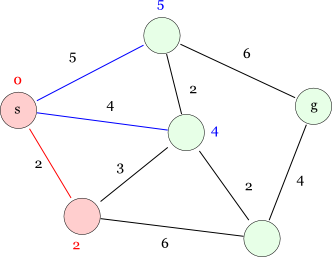
では，新たに確定したノードから辿れる経路をチェックしてみましょう。この左下のノードから辿れるのは中央のノード，右下のノード，（無向グラフなので）スタートノードの3つがあります。左下のノードからこれらのノードに辿った場合の距離を緑色で書き添えてみます。

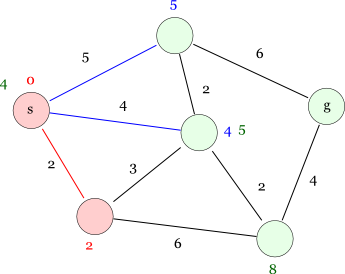
ここで，スタートノードにまた戻るような経路は全くの無意味なのではじきます。なぜ無意味なのかというと，そのような経路は（全てのエッジのコストが正であれば）最短経路とはなりえないからです。最短経路となるのは，そこまでの距離がより少ない経路のみを考えればいいので，今まで判明している最短距離よりも大きいような経路は捨ててしまってかまいません。そうすると，中央のノードへはスタートノードから直接行く距離 4 の経路さえ覚えておけばいいわけです。今まで分かっている中で最短の経路のみを記憶するので，判明している最短経路の図は次のようになります。

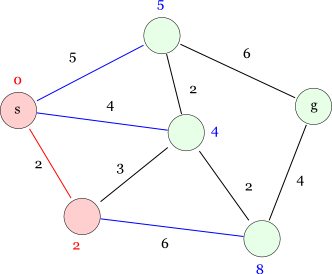
次は距離4の中央のノードが（未確定ノードのうち）最短なので確定できます。そして，中央のノードからは4つのエッジが伸びているので，それぞれ中央のノードを経由した（スタートノードからの）距離を計算します。

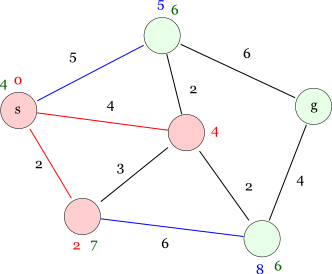
ここで，右下のノードは新たな最短距離候補が見つかったので，以前のデータを破棄して新たな経路を採用します。他の経路は最短ではないので更新しません。

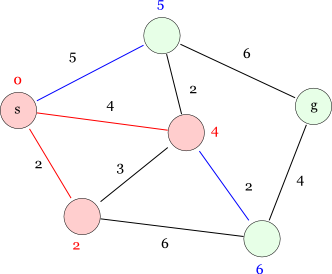
今までの手順と同様に，上の距離5のノードを確定して，最短経路候補を更新します。

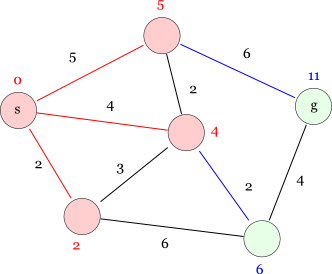
次に，右下の距離6のノードが確定して，最短経路候補が更新されます。

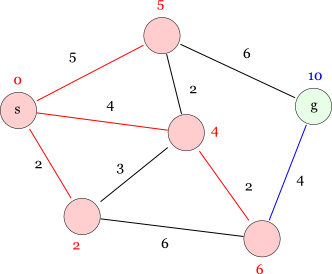
最後にゴールノードが確定して，全てのノードへの（スタートノードからの）最短距離が確定します。

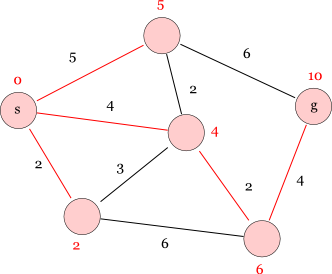
以上で，「スタート→中央→右下→ゴール」という経路が最短で，その距離は10であるということが求まりました。これがダイクストラ法です。

アルゴリズムを簡潔にまとめると，次のようになります。

初期化：スタートノードの値（最小コスト候補）を0，他のノードの値を未定義（または∞）に設定。
確定ノードをピックアップすることができなくなるまで（＝変化がなくなるまで）以下のループを繰り返す：
1. まだ確定されていないノードのうち，最小の値を持つノードを見つけ，確定ノードとする（確定フラグを立てる）。
2. 確定ノードからの伸びているエッジをそれぞれチェックし，「確定ノードまでのコスト＋エッジのコスト」を計算し，そのノードの現在値よりも小さければ更新する（経路情報も必要であれば，「どこから来たのか」を表す変数が確定ノードを指すようにする）。

経路を取り出す場合は，ゴールノードから「どこから来たのか」を逆順に辿っていって，それをひっくり返すことでスタートからゴールへの順路が得られます。

ダイクストラ法の特徴としては，

負のコスト（距離or時間）を持つエッジは扱えない
特定のノードからの最短距離およびその経路が全てのノードに対して求まる

などが挙げられます。

アルゴリズムの実装

ダイクストラ法には色々な実装方法があります。まず，最小の値を持つ確定ノードを選択する方法に「全てのノードを調べる」単純な方法と，「優先度付き待ち行列（プライオリティ・キュー）」を使った方法があります。また，ノードやエッジの情報をどのように格納するかによって，プログラムの書き方が少し変わってきます。

ダイクストラ法ではノードを中心にエッジを参照するので，エッジの情報はそのエッジの接続元ノードに格納しておくとアクセスしやすくなります。例えばC++であれば，

struct Node {
  // このノードから伸びるエッジの情報
  vector<int> edges_to;    // 各エッジの接続先のノード番号
  vector<int> edges_cost;  // 各エッジのコスト

  // ダイクストラ法のためのデータ
  bool done;  // 確定ノードか否か
  int cost;   // このノードへの現時点で判明している最小コスト
};

というような構造体でノードを表現すると分かりやすいでしょう（エッジ情報を pair や struct で構造化してもいいのですが，ここではその後に変更しづらくなるのでおすすめしません）。これは有向グラフの表現なので，無向グラフの場合は逆側の有向エッジも設定しておく必要があります。

上のデータ構造を使って，「全てのノードを調べて」確定ノードを決定する場合，アルゴリズム（擬似コード）は次のようになります：

// 初期化
foreach node in nodes:
  node.done = false
  node.cost = -1

nodes[start] = 0 // スタートノードのコストは0

// アルゴリズム実行
loop:
  // 確定ノードを探す
  doneNode = null // 確定ノード
  foreach node in nodes:
    if node.done or node.cost < 0:
      continue
    if doneNode == null or node.cost < doneNode.cost:
      doneNode = node
  // 確定ノードがなくなれば終了
  if doneNode == null:
    break

  // 確定フラグを立てる
  doneNode.done = true
  // 接続先ノードの情報を更新する
  for i = [0, doneNode.edges_to.size()-1]:
    to = doneNode.edges_to[i]
    cost = doneNode.cost + doneNode.edges_cost[i]
    if nodes[to].cost < 0 or cost < nodes[to].cost:
      nodes[to].cost = cost

強調表示部分が「全てのノードを調べて」いるところです。また，優先度付き待ち行列を使うと次の擬似コードのようになります：

// 初期化
foreach node in nodes:
  node.done = false
  node.cost = -1
PriorityQueue q // 優先度付き待ち行列

nodes[start] = 0 // スタートノードのコストは0
q.push(nodes[start])

// アルゴリズム実行
while not q.empty():
  // 確定ノードを取り出す
  doneNode = q.pop()

  // 確定フラグを立てる
  doneNode.done = true
  // 接続先ノードの情報を更新する
  for i = [0, doneNode.edges_to.size()-1]:
    to = doneNode.edges_to[i]
    cost = doneNode.cost + doneNode.edges_cost[i]
    if nodes[to].cost < 0 or cost < nodes[to].cost:
      nodes[to].cost = cost
      if not q.contain(nodes[to]):
        q.push(nodes[to])

「全てのノードを調べる」方法と違っているところを強調表示しています。なお，この他に「優先度」を表すために「ノードの大小」を判別するためのコードが必要になるでしょう（例えばC++の場合は struct Node 内で比較演算子をオーバーロードします）。

また，単に最短距離だけでなく最短「経路」を求める必要がある場合は，struct Node に int from を足して「どのノードから来たか」を表せばOKです。

データ構造としては，上のように各ノードにエッジ情報を持たせるのではなく， 2次元配列で隣接行列（接続ノード間の距離を記載した表）を保持しても構いません。当然，疎な行列の場合はメモリを無駄に食います。

補足1: 負のコストを持つエッジが一つでも存在すると，この推論が成り立たなくなります。ダイクストラ法は「全てのエッジのコストが 0 以上であること」が条件です。

$Id: index.shtml 1444 2007-04-19 13:05:50Z SYSTEM $

deq notes