Square Route 解説
- 問題名:Square Route [スクウェア・ルート]
- 出典:Problem D, ACM/ICPC Practice Contest for Japan Domestic, 2007-06-24
- 難易度:☆☆☆
- 問題の種類:幾何
- 解法:辺の長さで分類 or ナナメ45度線
- 解答ソースコード:
- p0107-deq_binsort.cpp(「辺の長さで分類」vectorによるビンソート版 O(N2))
- p0107-deq_binsort_map.cpp(「辺の長さで分類」mapによるビンソート版 O(N3) → 同じ長さの辺が多いので高速)
- p0107-deq.cpp(「辺の長さで分類」クイックソート版 O(N3)
- p0107-deq_diag.cpp(「ナナメ45度線」vectorによる数え上げ)
- p0107-deq_diag_map.cpp(「ナナメ45度線」mapによる数え上げ)
- OB/OGの会の解説:p0107-obog.pdf
素朴な全探索アルゴリズム
道が水平・垂直に走っていて,それらによって「正方形がいくつ作られるか」を求める問題。
まず,縦軸の各点から2点を取り出す組み合わせは N2 通りあります。 横軸の各点から2点を取り出す組み合わせも同様に M2 通りです。 ですから,全探索をすると組み合わせ総数が O(N2M2) になります。 ここで N, M ≦ 1,500 なので,N = M = 1,500 を代入すると最悪計算量が 1,5004 ≒ 5,000G となって,まず解けません。
以下,簡単のため N = M とみなします。 すると,先ほどの計算量は O(N4) です。 もし計算量が O(N3) の場合は 1,5003 ≒ 3G となり, 計算量が O(N2) の場合は 1,5002 ≒ 2M になります。
O(N3) の場合は解けるかどうかがいまいち分かりませんが,データセットによっては解けそうな計算量です (上の概算は最悪計算量なので,実際の計算量はもっと低いことが予想されます)。 O(N2) の場合は確実に解けることが分かります。 この計算により,この問題には(ICPC的に解ける問題である以上)O(N2)~O(N4) で解を与えるアルゴリズムが複数存在し, おそらく最適解のアルゴリズムは O(N2) で,少なくとも O(N3) のアルゴリズムを見つける必要がある,ということが分かります。 ちなみに O(N2 log N) であれば計算量はだいたい 1,500×1,500×10 ≒ 23M になるので,O(N2 log N) のアルゴリズムが見つかればそれも適切なアルゴリズムの一つであろうことが分かります。
今までの計算は,問題を解くアルゴリズムを考える前, もしくはアルゴリズムを考え付いた後に計算量を求める際に, そして少なくともコーディングを始める前に解析しておくべきことがらです。 例えば O(N3) のアルゴリズムが見つかったとしても,それで解けるかどうかはやってみないと分かりません。 ですので,O(N2) のアルゴリズムを考える必要があるか, とりあえず試してみるかのどちらかを「冷静に選択する」必要があります。 思いついたからといってすぐにコーディングを始めないように!
さて,種明かしをすると,実際にはこの問題は O(N3) のアルゴリズムで解けます。 というのも,この問題は国内予選形式,すなわち各自のPC上で計算して答えだけをアップロードするように出題されたので,数十秒かかっても答えが出ればOKなのです。 これを見極めるには,一度データセットをざっと眺めたり行数をカウントしたりするのがいいでしょう。
この問題を解くアルゴリズムは色々考えられますが, 以下では代表的な O(N2) のアルゴリズムを2つ取り上げて解説します。
辺の長さで分類
辺の長さのみに着目し,縦横の辺の長さで分類し一致しているかどうかを見ることによって計算量を O(N2) まで削減する方法です。 これはすなわち,この問題を解くためには本質的に各正方形の位置情報(座標)や出現順序の情報は不要であり, それらを扱わないことで O(N4) で行っていた不要な計算を省略しているということを意味しています。 これは,この問題が格子状であることからくる利点になっています。
アルゴリズムの概略
サンプル入力の最初のデータセットに含まれる正方形の図を見てみましょう。
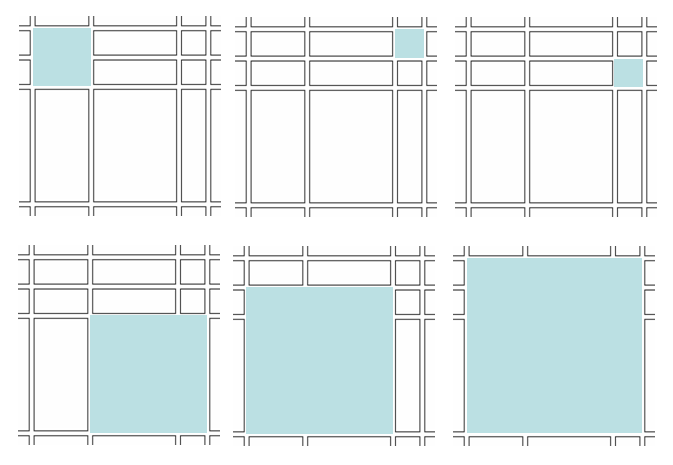
ここでは,複数の道を跨いだ正方形も考慮されています。 これは面倒なので,複数の道を跨がない正方形のみをカウントすればよいように図を描き換えます。 これは,縦側に含まれる N2 個の全ての辺と, 横側に含まれる M2 個の全ての辺を一つずつ描くことで可能になります。
上の例では,含まれる辺は次のように列挙することができます:
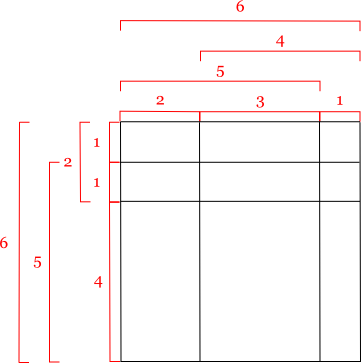
これらの辺 V = {1, 1, 4, 2, 6, 5}, H = {2, 3, 1, 5, 6, 4} を次のように展開します。
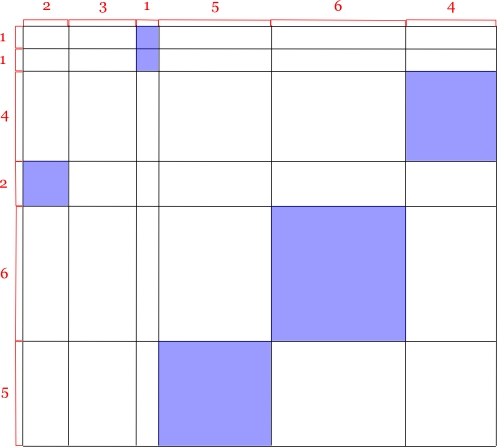
これで線を跨ぐ必要無く計算できます。 ちなみに色を塗っているところが正方形になっています。 さて,ここでこれらの組み合わせを全て調べれば, 縦側の辺が N2 個,横側の辺が M2 個で, 結局 O(N2M2) = O(N4) の計算量になってしまいます。
しかし,このように展開すると,明らかに辺の順序が関係無いことが分かりますので, これらの辺を並べ替えても(ソートしても)問題ありません。
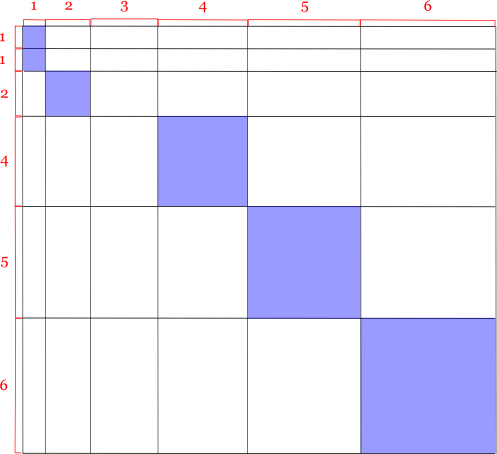
こうすると,行列の対角要素があるかないか,という感じで視覚的イメージで理解できるでしょう。 全ての組み合わせ(行列の要素数 = O(N4) 個)について調べる必要はなく, 対角要素辺りに位置するものだけ(対角要素の数 = O(N2) 個)を調べればいいので,その分だけ計算量を大幅に減らすことができます。 具体的には,各辺の長さに対して(縦側の同じ長さの辺の数)×(横側の同じ長さの辺の数)を求めて, それを全て足し合わせれば全体の正方形の合計になることが分かります。
アルゴリズムの計算量
最初に,縦側と横側の両方について,各辺の長さを全て求める必要があります。 これは O(N2 + M2) = O(N2) の計算量になります。 できあがった辺の数もそれぞれ最大 N2 になります。
次に,各辺をソートする必要があります。 これは,通常の O(n log n) のソートを用いると O(N2 log2 N2) = O(N3) になってしまいます。 しかし,値の範囲が 1~1,500×1,000 にあるのが分かっているので,O(n) のビンソート (bin sort) を使うと O(N2) の計算量で済みます。 この場合,ビンソートは結局のところ辺の長さの頻度分布(ヒストグラム)を求めていることになります(この説明はwosugiさんに感謝)。
最後に,正方形の数を数え上げる必要があります。 通常のソートをしてデータが配列や二分木 (TreeMapまたはSTLのmap) などに入っている場合はその要素数個(最大 O(N2 ) 個)で, ビンソートをした場合は計算量は固定で 1,500,000 ≒ N2 (N ≦ 1,500 なので) になるので, 正方形の数え上げにはだいたい O(N2) 程度かかることになります。
以上より,全体の計算量は,ビンソートをした場合は O(N2) で済むことが分かります。
アルゴリズムの実装
アルゴリズムの実装は非常に単純で,ビンソートの場合のアルゴリズムは次のような擬似コードになります:
h and w are the input vectors
reset V[1,500,000] and H[1,500,000] with zeros
for i = [0, h.length):
len = 0
for j = [i, h.length):
len += h[j];
V[len]++
for i = [0, w.length):
len = 0
for j = [i, w.length):
len += w[j];
H[len]++
count = 0
for i = [1, 1,500,000]:
count += V[i] * H[i]
ナナメ45度線
ナナメ45度の線を使って,各交点を分類する手法です。 「辺の長さで分類」では辺の長さに着目して分類することで順序情報などを省いて高速なアルゴリズムを導きましたが, ここでは「どのナナメ45度線に属するか」で分類することで必要な情報のみを使って計算する高速なアルゴリズムを導きます。
アルゴリズムの概略
まず,各交点の座標を計算しておきます。 これは入力時に処理しておくと簡単です。
次に,各交点がどの45度の線に属するかを求めます。 45度の線といえば当然 y = x + b で, 出題図に倣って左上が (0, 0) で右下が正の方向を考えると, これは右下に向かって延びる45度線になります。
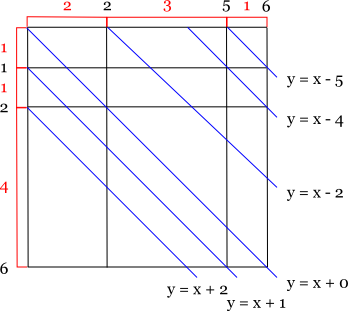
そして,y = x + b を式変形して得た b = y - x で,各交点を分類することができます。 正方形を構成する左上の点と右下の点は当然同じ45度線上にあり, 逆に同じ45度線上に点が2つ以上あれば正方形が構成されます。 いくつ正方形が構成されるかというと,1点であれば0個,2点であれば1個,3点であれば3個は当然として, 一般的なケースでは n 点から 2 つの点を取る組み合わせ数に等しいので, nC2 = n (n - 1) / 2 個になります。 後はこれらの点を全てのナナメ45度線に対して計算すれば最終的な答えが求まります。
アルゴリズムの計算量
y - x = b で分類する際の点の個数をカウントする際に,b の値をキーに,その個数を値とする key-value ペアを表現できる実装方法が必要です。 一般的に,key-value ペアの実装には追加および参照が O(1) のハッシュテーブルか O(log n) の二分木が使われます。 ここではハッシュテーブルの代わりに値の範囲 [-1,500×1,000, 1,500×1,000] に対応する 3,000,000 個の配列を使うことでハッシュ計算の手間を省くことができます。 二分木は,C++のSTLでは map を使って実装することになるでしょう。
ハッシュテーブル(あるいはその代替物)を使う場合, O(N2) 個の各交点全てに対して b = y - x を求めてハッシュテーブルに格納するのに必要な計算量は O(N2) です。 また,そこから正方形の個数を数え上げるのに必要な計算量は一定で 3,000,000 回になります。 N = 1,500 と仮定すると,3,000,000 ≒ N2 程度なので,全体の計算量は O(N2) になります。
二分木(あるいはその代替物)を使う場合, O(N2) 個の各交点全てに対して b = y - x を求めて二分木に格納するのに必要な計算量は O(N2 log N2) = O(N3) です。 また,正方形の個数を数え上げるのに必要な計算量は,存在する b = y - x の数が最大 O(N2) なので必要な計算量は O(N2) になります (二分木は一つだけを見つけようとする場合は O(log n) かかりますが,全てを列挙する場合は O(1) と見なせます)。 結局,二分木の場合の最悪計算量は O(N3) になります。 ただし,ここで「ナナメ45度線 (= b) がいくつ存在するか?」というと,b の値には実際には重複が多く, b が実際に取る値の種類数を B で表すと B << N2 が期待できます。 もし例えば B が N 程度しかなければ,全体の計算量は O(N2 log B) = O(N2 log N) となって, ここで N は十分に小さいので O(N2) と大差ない計算量になります。 ここらへんの仮定はデータセットに依存するので本当のところは何とも言えませんが, それほど悪くないであろうことは推測程度ではありますが一応推察できます。
アルゴリズムの実装
アルゴリズムの実装は非常に単純で,二分木 map を使った場合のアルゴリズムは次のような擬似コードになります:
ys and xs are the coordinates
diag = new map<int, int>();
for x in xs:
for y in ys:
diag[y - x]++
count = 0
for k, v in diag
count += v * (v-1) / 2
その他のアルゴリズム
ジグザグ歩き法がOB/OGの会の解説にあります。
$Id: index.shtml 1580 2007-06-28 05:20:33Z SYSTEM $