プリム法(最小全域木問題)
プリム法 (Prim's MST Algorithm) は最小全域木問題を効率的に解くグラフ理論におけるアルゴリズムです。
最小全域木 (MST: Minimum Spanning Tree) とは,グラフを構成する「辺の重みの総和」が最小となる全域木です。 「全域」とは,元のグラフがあって,その部分グラフのうち(辺の構成は変わっていても)頂点集合が同じグラフを指します。 木とは連結 (connected) でかつ閉路 (loop) が無いグラフなので,つまり,元となる(木ではない)グラフがあって, そこから,切り離された頂点を作らずに(連結であり),閉路を作るような辺が「辺の重みの総和が最小となるように」全て取り除かれた(木である)グラフを求める問題です。
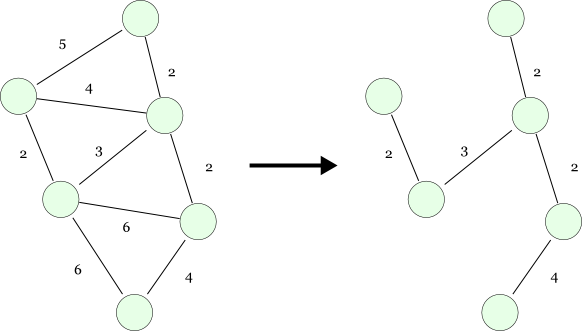
MST(最小全域木)を求めるアルゴリズムとしては,ここで説明するプリム法の他にクラスカル法が有名です。
アルゴリズム
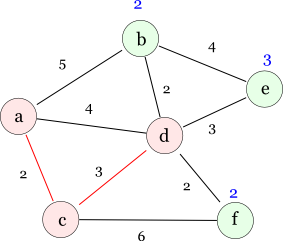
以下のグラフを例にプリムのアルゴリズムを解説します。 円がノード(頂点)で,ノード内のアルファベットは便宜的に付けたノードの名前です。 線がエッジ(辺)で,エッジの近くの数字はそのエッジのコストを表しています。 ここではエッジに向きが存在しない無向グラフです。
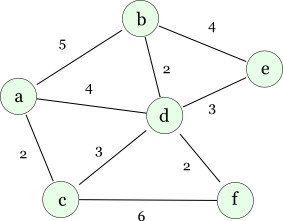
現実の問題としては,例えばノードとしては都市,エッジは都市間を結ぶ道路や橋の建設費用と考えると良いでしょう。
距離行列
まず,距離行列 (distance matrix) があるとアルゴリズムの説明上便利なので,グラフから距離行列を作ります。 距離行列は2つのノード間の距離を2次元の表にしたものです。 繋がっているか繋がっていないかを重視する場合は隣接行列 (adjacency matrix) とも呼びます。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 0 | 5 | 2 | 4 | ∞ | ∞ |
| b | 5 | 0 | ∞ | 2 | 4 | ∞ |
| c | 2 | ∞ | 0 | 3 | ∞ | 6 |
| d | 4 | 2 | 3 | 0 | 3 | 2 |
| e | ∞ | 4 | ∞ | 3 | 0 | ∞ |
| f | ∞ | ∞ | 6 | 2 | ∞ | 0 |
通常,自分自身への距離(例えばaからaの距離)は0になります。 また,直接エッジが伸びていないノード間の距離は,どのような数よりも大きい値を設定しておきます。 数学的にはそれは無限大 (infinity) のことなので,上の表では∞を記入しています (実装する場合は -1 や INT_MAX を使うことになるでしょう)。
なお,無向グラフの場合,bからdへの距離とdからbへの距離は等しいので,距離行列は下図のように対称行列 (symmetric matrix) になります。 距離行列を実装する場合,上三角行列か下三角行列のどちらかだけ保持すれば十分ですが, ICPC的にはメモリが足りなくなることはまずないので,特に気にせず全て記憶しておくとソースコードが短くなってバグも減りやすくなります。
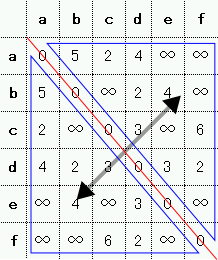
解法のアイデア
プリム法は,ダイクストラ法と同様に,DP的なアルゴリズムです*1。 つまり,「まずサイズ k=1 の場合を求め,そこから順に k を増やして求めていく」手法です。
ここでは,ノードが1つの場合 (k=1) のMSTを求め,そこから k=2 の場合のMSTを求め…と解いていきます。 まず,k=1の場合は,どのノードを選んでも一緒ですので,ここではとりあえずノード a を選びます。
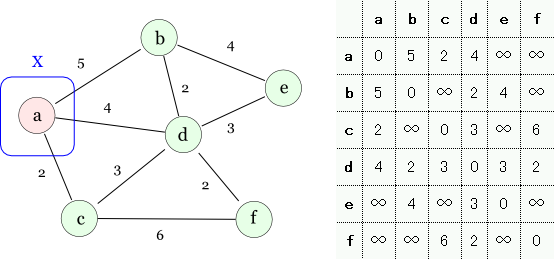
この時点で,ノードの集合として X = {a} だけを見ると,エッジのコストの総和は 0 で,これはMSTになっています。 まぁ,当然ですね。 次に,ここから考えて,ノードが一つ増えてもMSTになっているように,エッジを一本選びます。
さて,全体としてMSTが構成されている場合,aからは少なくとも一本エッジが生えているはずです (一本も生えていなかったら,それは木になっていませんから)。 MSTの場合,それがどのノードに繋がっているかは重要ではありません。 とにかく木にぶらさがっていればいいので,できるだけ少ないコストで,MSTである木に繋がっていればOKなはずです。
ここで a から伸びているエッジは E(a) = {a-b: 5, a-c: 2, a-d: 4} だけなので,最小コストを持つ c へのエッジを選択します。
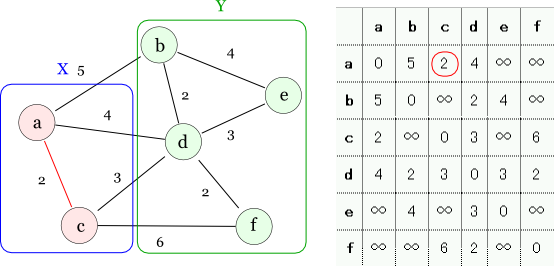
これで,ノードの集合として X = {a, c} だけを見ると,エッジのコストの総和は 2 で,X内でちゃんとMSTになっています。 ただし,このアルゴリズムが正しいというためにはそれだけでは不十分で, 「このX内のMSTがノード集合全体 V を構成するMSTの部分グラフになっている」ことを述べる必要があります。 そうでないと,新しくノードを追加したときにエッジの付け替えをしないといけない,つまりは後戻りをしなければならない可能性があるということで,それはDPの原則に反して計算量が多くなります。
さて,このXが求めたいMSTの部分グラフになっているかどうかを背理法で見てみましょう。 ここではノードaとcを結ぶ最小のエッジとしてエッジa-cを選択しましたが,これが間違いだったとします。 つまり,エッジa-cはノードaとcを結ぶ最小コストの経路ではなく, より少ないコストを持つ「a → c以外のノード(1つ以上) → c」というような経路が存在すると仮定します。 しかし,エッジa-cのコストはaが持つエッジの中で最小なので,もしグラフ中に負のコストを持つエッジが存在しなければ, エッジa-cを使わない経路は必ずエッジa-cよりもコストが高くなります(一般的には,コスト0のエッジが存在する場合は,同じか高くなります)。 従って,最初に仮定したような経路は存在せず,結局「ノードaとcが最小コストの経路で繋がっているとすれば,エッジa-cを通じて繋がっている」ことが証明できました。 求めたいMSTではノードaとcは必ず何らかの経路で繋がっているので,このXは求めたいMSTの部分グラフになっています。
では次のステップに行きましょう。 考え方は前回と一緒で,「ノードが一つ増えてもX内でMSTで,かつ全体のMSTの部分グラフとなっているような」エッジを一本選びます。 具体的には「ノード集合 X のいずれかとノード集合 Y のいずれかを繋ぐエッジのうち,最小コストのエッジ」を見つけます。 XからYに伸びているエッジ集合は E({a, c}) = {a-b: 5, a-d: 4, c-d: 3, c-f: 6} の4本なので,このうち最小であるコスト3のエッジ c-d を選択します。
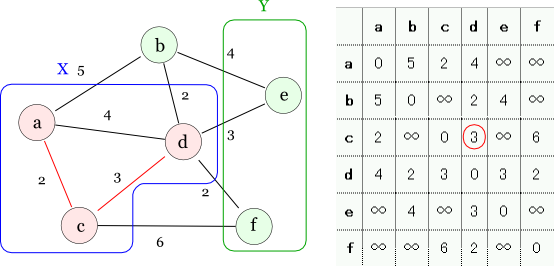
これでノード集合 X = {a, c, d} は,それ自身MSTであり,かつ全体のMSTの部分グラフになっています(エッジのコストの総和は5)。 証明は,前回と同様に X' = {a, c} と Y' = V - X' = {b, d, e, f} に対して背理法を適用すればOKです。 その証明を一般化して数学的帰納法として定式化すると,このアルゴリズムが上手く行く理由が説明できます。
一応,上記のアルゴリズムを最後まで適用して,結果を見てみましょう。 ここで「Xの要素 → Yの要素」の最小コストのエッジは d-b と d-f の2つ存在しますが,これはどちらを選んでも問題ありません。 ここではアルファベットの小さい方を選んで,エッジd-bを選択してみましょう。
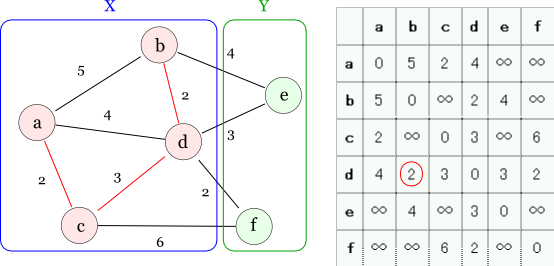
これでエッジのコストの総和が7のMSTになっています。 さらに,同様に「Xの要素 → Yの要素」の最小コストのエッジ d-f を選択します。
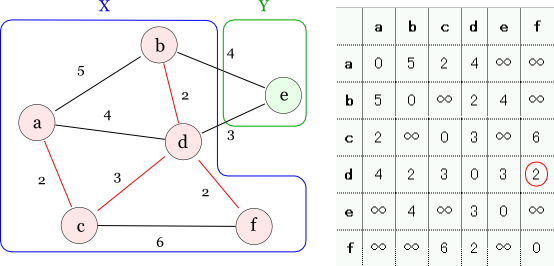
これでエッジのコストの総和が9のMSTになっています。 最後に,同様にノード d-e を繋ぎます。
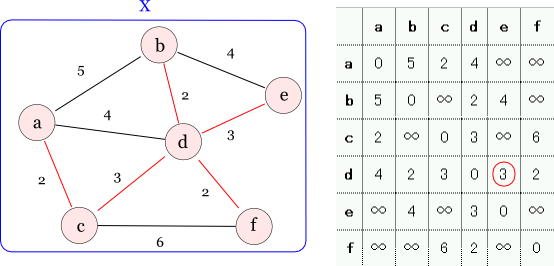
これでMSTが完成しました。エッジのコストの総和は12です。 ちなみに要らないエッジを取り除くと,このMSTは次のようになっています。
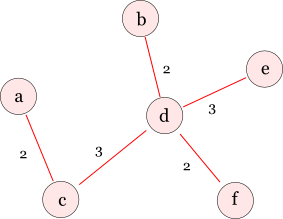
以上が,プリム法の基本的な考え方です。
アルゴリズムを簡潔にまとめると,次のようになります。
- 初期化:X = {a}, Y = V - X とする(ここでノード a は何でも良い),エッジのコストの総和を0とする
- Y が空になるまで以下のループを繰り返す:
- 「Xの要素 → Yの要素」を繋ぐエッジのうち,最小コストを持つエッジ e を探す(この実装方法は後で詳述)
- X = X + {eのY側の要素}, Y = Y - {eのY側の要素} とする(実際にはノードの確定フラグを立てればよい)
- エッジのコストの総和にeのコストを加算
ここで,XとYを繋ぐ最小コストのエッジを見つける手法によって, 全ノードの数を|V|,全エッジの数を|E|とすると,計算量が O(|V|3), O(|V|2), O(|E|⋅log|V|) と異なってきます。 この違いは重要ですので,次にそれぞれの実装方法を見ていきます。
アルゴリズムの実装
素朴な方法
まず,素朴な方法 (naive method) です。 XとYを繋ぐ最小コストのエッジを見つける必要があるたびに(|V|回のループ), Xの要素から伸びているエッジを毎回全て調べ,その中で最小コストのエッジを見つけることができます。 ループの内側では,これは最大でも毎回全エッジを調べれば済むので,O(|V|2) もしくは O(|E|) になります。 これが |V| 回ループで回るので,全体の計算量は O(|V|3) もしくは O(|V|⋅|E|) になります。
ノード数が100であれば |V|3 = 1,000,000 = 1M で解けそうですが, ノード数が1000になると |V|3 = 1,000,000,000 = 1G で解けなくなります。
各ノードへの最小コストを記憶・更新する方法
次に,ダイクストラ法と同じような感じで,Yの各要素に現時点での最小コストを記録しておく方法があります。 例えば,上述の例題グラフでは,初期化フェーズでノード a を選んだ際に, a から1ホップで直接到達可能なノードを次のように設定します。
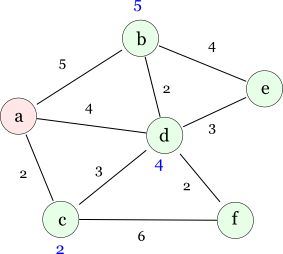
次に加えるノードを選択することになりますが,その際には全てのノードを調べ, 記録しているコストが最も小さいものを選びます。 ここではノード c ですね。 ノード c を選んだ際には,ノード c から直接到達可能なノードに対して, 今現在の最小コストよりもノード c から直接到達可能なコストの方が小さければ, それらのノードの最小コストを更新します。 具体的には次のように更新されます(ノード d の最小到達可能コストが更新されたことに注意)。
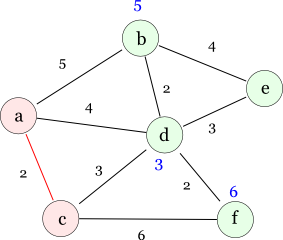
次に加えるノードは,また全ノードの値を比較して最小値を求めればよいので,ここではコスト3のノード d になります。 ノード d から直接到達可能なノードの値を更新すると次のようになります。
次に加えるノードは b か f になりますね。 さて,この場合,まずループ自体は |V| - 1 回まわるので O(|V|) です。 ループの内側では,追加ノードの選択は全てのノードを調べるので |V| 回で,ノードの更新はそこから伸びているエッジの数なので最大 |V| 回になります。 従って,ループの内側は |V| + |V| → O(|V|) になって,全体としては計算量は O(|V|2) になります。
ノード数が1000くらいまでであれば,|V|2 = 1,000,000 = 1M で解けそうですね。
優先度付き待ち行列
上記の方法でもたいていの場合は十分高速ですが,ダイクストラ法と同様に, プリム法でも優先度付き待ち行列 (priority queue) を使うことでさらなる高速化が可能です。
実装も比較的簡単で,まず最初に初期化フェーズでノード a を選択後,a から伸びているエッジを全て優先度待ち行列に追加します。 優先度付き待ち行列はエッジのコストでソートされるようにしておきます(内部構造にヒープ (heap) を使うと追加は O(log n) になります)。 次に,優先度付き待ち行列から取り出した(popした)エッジの接続先ノードを,現在のMSTに追加します(pop も O(log n) で可能です)。 そして,そのノードから伸びているエッジをまた全て優先度付き待ち行列に追加していきます。 なお,popしたエッジの接続先がすでにMSTに追加済みなら気を取り直してもう一度popし直します。 後はこれを繰り返すだけで動きます。
この場合,ループ回数はすなわち優先度付き待ち行列に挿入される回数なので, 上のアルゴリズムではエッジは全て各2回ずつ挿入されるので |E| になります。 ループの内側では,挿入 = O(log n) とpop = O(log n) だけなので,二つの操作を足して O(log n) になります。 ここで n は待ち行列の長さですが,最大 |E| を超えることはないので, O(log |E|) とみなせます。 結局,全体としては計算量は O(|E|⋅log |E|) となります。
なお,これは見境なく待ち行列にエッジを追加しているので, 重複しているノードに対するエッジは待ち行列内で置き換える,なんていう操作をしてあげると待ち行列の長さが最大 |V| となって, 計算量も O(|E|⋅log |V|) に落ちますが(通常 |V| < |E| が成り立つので),実装は面倒になります。
計算量を O(|E|⋅log |E|) とすると,ノード数が100の完全グラフの場合はだいたいエッジ数が5000程度で |E|⋅log2 |E| = 350,000 = 350K 程度(ただしこの種の計算はかなり大雑把ですが)。 ノード数が1000の完全グラフの場合はだいたいエッジ数が500,000程度で |E|⋅log2 |E| = 350,000,000 = 350M 程度になるようです(なお O(|E|⋅log |V|) であれば 15M 程度)。 これを見る限り,完全グラフのように距離行列が十分に密であれば,最小値を更新する方法で良いでしょう。 なお,フィボナッチヒープを使うと O(|E| + |V| log |V|) で実装できるようですが,そこまでシビアな問題がICPCで出るとは思われません。
補足1: また,貪欲法 (greedy algorithm) の一種であるとも考えられます。 貪欲法は,各ステップごとにそのステップでの最適経路を求め,それ以外の経路を枝刈りする探索手法です。 各ステップごとで最適であっても,問題全体で最適とは限らないため,局所最適解は得られても全域最適解が得られるとは限りません。
DPというのは,貪欲法でそのように求めていった場合,全域最適解が得られることが保証されているアルゴリズムを指します。 ですから,DPは貪欲法の一種である,といえます。 ただし,個人的には,わざわざ貪欲法という言葉を使う場合,DPを除く,すなわち最適解が得られる保証はない場合の解法を指したいときに使っています。
$Id: index.shtml 1496 2007-05-11 19:08:56Z SYSTEM $