ベクトルの基礎

デカルト座標系とユークリッド空間

まずは基本的な用語から。 私たちが通常使っている直交座標系のことをデカルト座標系 (Cartesian coordinate system) とも呼びます。 x, y の値は両方とも実数です（x, y ∊ R）。 デカルト座標上の2点 a, b の距離をピタゴラスの定理（三平方の定理）

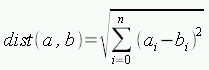
dist(a, b) = sqrt{sum from{i = 0} to{n} (a_i - b_i)^2}

で定義した空間をユークリッド空間 (Euclidean space) と呼びます。2次元のxy平面であれば，上式で n = 2 を代入して，距離は

dist(a, b) = sqrt{(a_x - b_x)^2 + (a_y - b_y)^2}

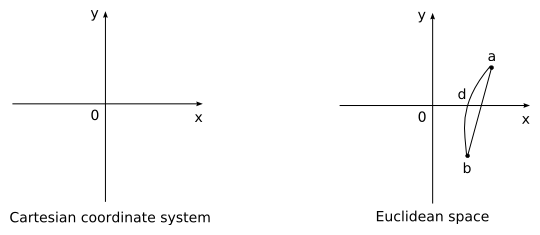
で求められます（下図の距離d）。 問題文章中にデカルト座標やらユークリッド空間（ユークリッド距離）やらという言葉が出れば， このような「通常」の空間だと思えばいいわけです。

スカラーとベクトル

スカラー (scalar) とは1つの値のことを指します。 例えば 3 (int) や -5.2 (double) といった値のことです。 Cでは文字列は配列なのでスカラーではありませんが，PerlやPythonなど，プログラミング言語によっては "abc" のような文字列もスカラーとみなせます。

ベクトル (vector) とは配列（あるいはリスト）のことを指します。 例えば2次元ベクトルは要素数が2で決め打ちの配列で表せます：

double a[2];

あるいは，2つのメンバを持つ構造体で表すこともできます：

struct vector {
  double x, y;
};

これらの違いは実装上の違いで大差はありません。 しかし，プログラミングで型が重要であるように，スカラー（値）とベクトル（リスト）という型の区別は行う必要があります*1。

点とベクトル

次に，点 (point) とベクトル (vector) の関係について考えます。 2次元平面上では，点は座標 (x, y) で与えられます。 構造体で書けば，

struct point {
  double x, y;
};

となります。 また，ベクトルは幾何学的には原点から与えられた点への（向きを持った）線分で表すことができます。 従って，1点を与えればただ1つのベクトルが定まりますし，1つのベクトルは1点を表しています。 すなわち，点とベクトルは同じようなものなのです。

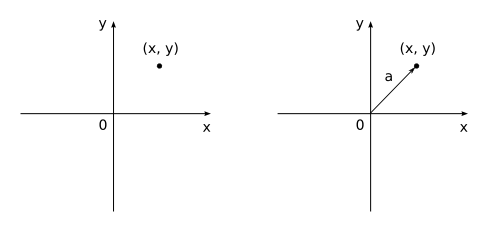
事実，上のコード例で載っているように，プログラム上のデータ構造は全く同一です。 ですから，ここでは点を表すデータ構造を用いてベクトルも表すことにします。 その方がプログラミングは楽になります。

なお，ベクトルは原点から点への有向線分だと述べましたが，同時に大きさと向きだけで表される量ともいえます。 注意すべきなのは，ベクトル自体には位置情報はない，すなわち平面上の線分を表すには始点の位置は別に持っておく必要があるということであり， ベクトル演算は座標位置を考慮した演算ではないということです。

ベクトルの和と差

ベクトル a, b の和 (sum, addition) c = a + b と 差 (difference, subtraction) c = a - b は次のように定義されます：

// 和：c = a + b
point sum(point a, point b) {
  point c;
  c.x = a.x + b.x;
  c.y = a.y + b.y;
  return c;
}

// 差：c = a - b
point sub(point a, point b) {
  point c;
  c.x = a.x - b.x;
  c.y = a.y - b.y;
  return c;
}

言い忘れていましたが，プログラミング言語はC++です。gccではなくg++でコンパイルしてください。

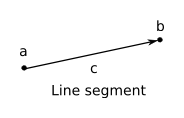
ベクトルの和・差は，幾何学的には下図のようなベクトルを生み出します。

これより，点 a, b を端点とする線分 (line segment) を表すベクトル c を作るには，終点から始点を引けばよいことが分かります (c = b - a)：

さて，上記ソースコードでは和・差のために sum() や sub() を定義しましたが，これでは和や差を多用するプログラムが少し見た目が複雑になってしまいます：

point d = sum(sub(c, a), sub(c, b));

これは次のように書けると直感的で幸せになれます：

point d = (c-a) + (c-b);

そこで，関数を定義するかわりに point 構造体に対して演算子を定義してみましょう：

struct point {
  double x, y;

  point operator+(point p) {
    point sum;
    sum.x = x + p.x;
    sum.y = y + p.y;
    return sum;
  }

  point operator-(point p) {
    point sub;
    sub.x = x - p.x;
    sub.y = y - p.y;
    return sub;
  }
};

このように定義すると + や - という演算子でベクトル演算をプログラミングすることができます。 これで少し幸せになれますが，逆に毎回これを書かないといけないという不幸せが生じます。 実はこれらのデータ構造と演算子を最初から定義しているC++の標準ライブラリがあります。 それが複素数を表すcomplex型です。 次回はcomplex型の導入から進めていきます。

補足1: なお，ベクトルは1次元配列です。 2次元配列のことは特別に行列 (matrix) と呼びます。 一般にn次元配列のことはn階のテンソル (tensor) と呼びます。 さらに突っ込んで言えば，それらは単なるデータ構造ではなく，メソッド（演算体系）もくっついているクラスといえます。

$Id: fundamental.shtml 1282 2007-02-03 09:05:17Z SYSTEM $