ベクトルの利用
complex型の導入
前回は構造体+演算子のオーバーロードでxy平面上の点(=ベクトル)を定義しましたが, ここで便利なC++標準ライブラリのcomplex型を導入します。 名前の通り,複素数を表現する型です。 使い方は次のような感じになります:
#include <complex> using namespace std; typedef complex<double> P;
ここでは(単にタイピングの量を減らすために)型の名前を以前のpointではなくPにしてみました。 名付け方は気分次第でしょう。 このcomplex型を使うと,上記だけの定義でベクトル演算を次のような感じで簡単に行えます:
P a(3, 5), b(4, -3); P c = (a - b) + P(1, 2);
和や差に関して,複素数の演算は2次元ベクトルの演算と等しいので,複素数を援用できるわけです。 これは,複素数平面上の点は2次元のユークリッド平面上の点と同じように扱える(直交座標系でかつユークリッド距離が適用される)ことに依拠します。 単に実軸 (real axis) をx軸,虚軸 (imaginary axis) をy軸と置き換えて読めばよいのです。
なお,complex型の実部と虚部はそれぞれ real() と imag() で取り出すことができます:
// 方法1 double x = a.real(); double y = a.imag(); // 方法2 double x = real(a); double y = imag(a);
a.x, a.y と書くよりも多少面倒ですがこの程度は我慢しましょう。 なお,代入は a.real() = 3.5; や cin >> a.real() などとします。
complexを用いて,2つのベクトル a, b(あるいは2点a, b)が等しいかどうかを調べるには, それぞれのx値とy値が等しいかどうかをチェックすればいいので,
// 2つのベクトルが等しいかどうか #define EQV(a,b) ( EQ((a).real(), (b).real()) && EQ((a).imag(), (b).imag()) )
とします。
なお,ここで関数 EQ は,
#define EPS (1e-10) #define EQ(a,b) (abs((a)-(b)) < EPS)
と定義しています。 これは,小数は計算誤差(丸め誤差)を持つために == では比較できないため,非常に小さい数 EPS 以下の差であれば同じとみなす,という処理をしています。 ここでは EPS は 1×10-10 としていますが,この値は問題に合わして変更する必要があるかもしれません。 とにかく,コンピュータで小数を扱う場合は常に計算誤差を意識する必要があります。
絶対値,2点間の距離,単位ベクトル
ベクトルの絶対値 (absolute value) もしくは大きさ(長さ)は,原点からそのベクトルが表す点までの距離で定義されます。 すなわち,2次元平面上では,2点間の距離
において,b が原点 = 0 であるとみなせばよいので,ベクトル a の絶対値 |a| は
となります。
complex型を使えば,絶対値は abs() で求めることができます:
// ベクトルaの絶対値を求める double length = abs(a);
また,2点 a, b の距離 (distance) はベクトル a-b の絶対値に等しい(あるいは b-a でも同じ)ので,2点間の距離は
// 2点a,b間の距離を求める double distance = abs(a-b);
で求めることができます。
2点間の距離を用いると,2点が等しいかどうかの判定は距離が0であるかどうかを調べればいいので
abs(a-b) < EPS
と書くことができます。 ただし,これは絶対値を求めているのでかなり遅いことに注意してください。 平方根を求める(sqrtを取る)のは重い処理なのです。
単位ベクトル (unit vector) は絶対値が1に正規化されたベクトルのことです(式で書けば |a| = 1)。 任意のベクトル a から同じ向きを持った単位ベクトル a を作るには,単にその絶対値で割って,
を求めてやればOKです。プログラムで書けば,
// ベクトルaの単位ベクトルを求める P b = a / abs(a);
となります*1
法線ベクトル,単位法線ベクトル
法線ベクトル (normal vector) とは,何かに対して垂直なベクトルという意味です。 よく使われるものに平面に対する法線ベクトルがありますが,これは3次元空間上での話なのでここでは扱いません。 2次元平面上では,あるベクトル(直線)に対して垂直なベクトル=法線ベクトルを考えることができます。 なお,法線ベクトルの大きさは気にしません(何でもよい,というか何をしたいかに依ります)。
ベクトルや直線に対する法線ベクトルというのは,下図(左)のように2つ存在します(a' と a'')。 図の (x, y) に (5, 2) などの数字を代入して図を描いてみれば簡単に分かりますが,法線ベクトルは次の式で求められます(ここでは大きさは元のベクトルと同じにしています):
// 1つ目 n1.x = -a.y; n1.y = a.x; // 2つ目 n2.x = a.y; n2.y = -a.x;
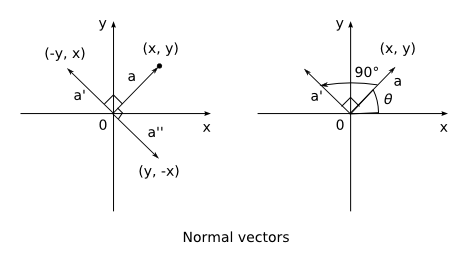
これはこれで難しくはないのですが,複素数の掛け算を使うとさらに簡単で間違いにくくなります。 複素数同士の積の結果は,「代数的には絶対値は積,偏角は和」となります。 偏角 (argument) とは(実軸からの)角度,すなわち上図(右)のθのことです。 数式で書くと,c = ab とした場合,|c| = |a| |b| でかつ arg(c) = arg(a) + arg(b) ということです。
つまり,絶対値が1の単位ベクトルを掛けると,絶対値を変えずにベクトルを回転させることができます。 法線ベクトルとは元のベクトルを90度回転させたものと-90度回転させたものですから, 90度に相当する複素数 i = (0, 1) や -i = (0, -1) を掛けてやれば法線ベクトルが求まります:
// ベクトルaの法線ベクトルn1,n2を求める P n1 = a * P(0, 1); P n2 = a * P(0, -1);
以上の2つを組み合わせると,単位法線ベクトル (unit normal vector) を求めることができます*2:
// ベクトルaの単位法線ベクトルun1,un2を求める P un1 = (a * P(0, +1)) / abs(a); P un2 = (a * P(0, -1)) / abs(a);
今回は以上です。次回はベクトルの内積・外積に進みます。
補足1: ちなみにcomplex型を使わなければ,
double absval = sqrt(a.x*a.x + a.y*a.y); b.x = a.x / absval; b.y = a.y / absval;
で求めることができます。
補足2: 単位法線ベクトルは2004年度の国内予選の問題で実際に使われました。
$Id: using_vectors.shtml 1509 2007-05-16 06:10:54Z SYSTEM $