内積と外積
内積・外積
ベクトルの内積 (inner product, dot product, scalar product) と外積 (outer product, cross product, vector product) という演算を用いると幾何の問題を解く考え方が簡単になります。 幾何学における内積や外積はもともと3次元空間上で定義されるものなので,まずは3次元空間上で幾何学的な内積・外積を導入し, それらが線形代数的なベクトル演算と等価であることを利用し,内積・外積を2次元平面上に拡張(縮小?)します。
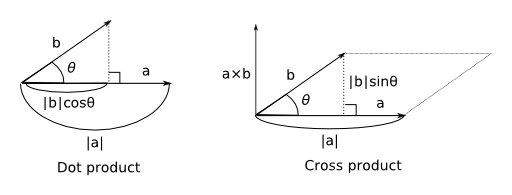
3次元空間上において,ベクトルの内積(ドット積)は a⋅b で表され, 以下の式で定義されます:
内積はcosを使って定義されている点と,内積の結果は単一の値=スカラーになる点に注意してください。
また,ベクトルの外積(クロス積)は a×b で表され, その大きさ |a×b| は
で与えられ,その向きは a, b を含む平面に垂直で, a から b への右ねじの進む向きになります。 外積はsinを使って定義されている点と,外積の結果はベクトルになる点に注意してください。 なお,定義より,外積の大きさはベクトル a, b が成す平行四辺形の面積になります。
また,内積は上式の他,次のベクトル演算によって求めることもできます:
外積も行列式 (determinant) を用いて次のように求めることができます(eは単位ベクトル):
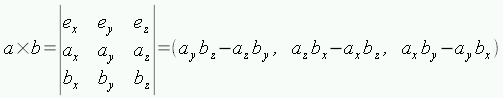
これらの式はcos/sinを用いた前式と等価ですが,計算は簡単になります。 さらに,これらは3次元空間上に定義されているので,z 値に 0 を代入すれば2次元平面上の内積・外積の式を導くことができます:
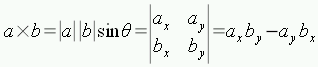
cos/sinを用いた定義はほぼ上式と同じですが,外積の結果は(ベクトルではなく)スカラーになっていることに注意してください。 2次元平面上の外積の結果は,必ず(3次元で言えば)zの値のみを持つベクトルとなるのでわざわざベクトルとはせずにスカラーとして扱う,という解釈でも良いでしょう。
ここではプログラム上では最後の2式を採用し,次のように関数を定義することにします (内積・外積はその演算子の形からドット積,クロス積とも呼ばれており,それがこれらの関数名の由来です*1):
// 内積 (dot product) : a⋅b = |a||b|cosθ
double dot(P a, P b) {
return (a.real() * b.real() + a.imag() * b.imag());
}
// 外積 (cross product) : a×b = |a||b|sinθ
double cross(P a, P b) {
return (a.real() * b.imag() - a.imag() * b.real());
}
ベクトルの内積・外積は様々な用途に使えるので,その性質と使い方を順に見ていきましょう。
2直線の直交判定・平行判定
2次元平面上のベクトルの内積・外積の幾何学的な定義をもう一度見てみましょう:
内積にはcos()が,外積にはsin()が使われています。 cos()は90度と-90度のときに値が0となるので,2ベクトルが直交しているときに内積は0になることが分かります。 ですから,ベクトルの直交判定に使うことができます。 同様に,sin()は0度と180度のときに値が0となるので,外積はベクトルの平行判定に用いることができます。 数式でこのことを宣言すれば,
a⋅b = 0 ⇔ a⊥b a×b = 0 ⇔ a//b
ということです。
2点 a1, a2 を通る直線または線分はベクトル a = a1 - a2 で表すことができるので, 直交判定と平行判定をするプログラムは次のようになります:
// 2直線の直交判定 : a⊥b <=> dot(a, b) = 0
int is_orthogonal(P a1, P a2, P b1, P b2) {
return EQ( dot(a1-a2, b1-b2), 0.0 );
}
// 2直線の平行判定 : a//b <=> cross(a, b) = 0
int is_parallel(P a1, P a2, P b1, P b2) {
return EQ( cross(a1-a2, b1-b2), 0.0 );
}
点が線上にあるかないかの判定
2点 a, b を通る直線と点 c が与えられたときに,点 c が直線 ab 上にあるかないかを判定することを考えてみましょう(下図の左)。
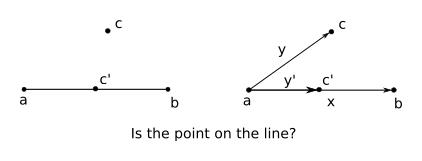
ここで直線を表すベクトル x = b - a と, 点 a から点 c に伸びるベクトル y = c - a を考えます(上図の右)。 上図から明らかなように,もし点 c が直線上にあればベクトル x とベクトル y は重なり, 点 c が直線上になければ重なりません(直線は長さが無限である点に注意)。 ベクトルが重なっているということは,それらのベクトルは必ず並行になっているといえます。 従って,点 c が直線 ab 上にあるかどうかは,前述の平行判定(外積が0かどうか)と同様に,
// 点cが直線a,b上にあるかないか
int is_point_on_line(P a, P b, P c) {
return EQ( cross(b-a, c-a), 0.0 );
}
と書くことができます。
次に,直線ではなく線分の場合を考えてみましょう。 つまり,2点 a, b を端点とする線分と点 c が与えられたときに,点 c が線分 ab 上にあるかないかを判定するということです。
まず,上述の直線の場合は必ず満たしていなければなりません。 しかし,線分には長さがあるので,直線 ab 上に乗っていても線分 ab の範囲からは外れている可能性があります。
単純に思い浮かぶのは,点 a,b と点 c の座標を比較する方法です。 点 c が線分上にあるためには,点 a, b を対角点とする長方形の中になければならないので(下図の左), 長方形の内か外を調べるコードを次のように付け足せばよいことになります (最初の行は,点 c が点 a や点 b に重なる場合,後の比較が(簡潔な表現をするためにEPSを用いていないので)計算誤差によって誤って判定されることを防いでいます):
// 点cが線分a,b上にあるかないか(1)
int is_point_on_line(P a, P b, P c) {
if ( EQ(abs(a-c), 0.0) || EQ(abs(b-c), 0.0) ) return 1;
if (a.real() < b.real()) {
if (c.real() < a.real() || b.real() < c.real) return 0;
} else {
if (c.real() < b.real() || a.real() < c.real) return 0;
}
if (a.imag() < b.imag()) {
if (c.imag() < a.imag() || b.imag() < c.imag) return 0;
} else {
if (c.imag() < b.imag() || a.imag() < c.imag) return 0;
}
return EQ( cross(b-a, c-a), 0.0 );
}

また,内積を使う(ちょっとややこしい)方法もあります。 cos()の結果は-90度~90度(右半円)であれば正,90度~270度(左半円)であれば負となります(上図の右)。 ですから,ベクトル x = b - a と ベクトル y = c - a の内積が正となれば, 点 a よりも線分側であると判定できます。 それを点 b と点 c についても行えばいいので,次のようなプログラムが書けます:
// 点cが線分a,b上にあるかないか(2)
int is_point_on_line(P a, P b, P c) {
return EQ( cross(b-a, c-a), 0.0 ) &&
(dot(b-a, c-a) > -EPS) &&
(dot(a-b, c-b) > -EPS);
}
計算誤差に対処するために,0.0 ではなく -EPS と比較していることに注意してください。
あるいは,三角不等式を使う簡潔な方法もあります。 もし点 c が線分上にあれば a→b の道のりと a→c→b の道のりは等しく, もし点 c が線分上になければ a→b の道のりよりも a→c→b の道のりの方が長くなります。
このことを素直にコーディングすれば,
// 点cが線分a,b上にあるかないか(3)
int is_point_on_line(P a, P b, P c) {
// |a-c| + |c-b| <= |a-b| なら線分上
return (abs(a-c) + abs(c-b) < abs(a-b) + EPS);
}
となります。
ここでは同じことをするアルゴリズムを3つ挙げましたが,最後に挙げた方法が最も簡潔で間違いにくく,使いやすいものでしょう。
さて,次回は直線(線分)と点の距離,線分の交差判定と交点計算を取り上げます。
補足1: 外積はクロス積のcrossではなく行列式のdetにしようかとも思いましたが, こちらの方が記憶しやすそうで混同しなさそうなのでcrossを採用しました。
$Id: products.shtml 1282 2007-02-03 09:05:17Z SYSTEM $