直線と線分

直線と点の距離

直線と点の距離は，点から「直線のどこか」への最短距離ですから， 点から直線へ垂線を下ろせばその垂線の長さが求めたい「直線と点の距離」になります。 それは，下図で示されているように，2点 a, b を通る直線と点 c との距離は， ベクトル x = b - a と ベクトル y = c - a を考えると，距離は

|d| = |y| |sin θ|

で求められます（sinはマイナスの場合もあるので絶対値を取っておきます）。

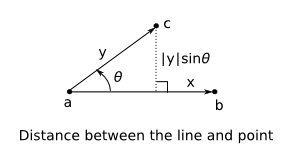
sinが入っているので外積の定義

x×y = |x| |y| sin θ

と見比べてみると，共通部分が多くあります。 両辺を |x| で割ると，

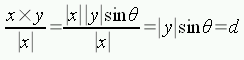
x×y / |x| = |x| |y| sin θ / |x| = |y| sin θ = d

となるので，直線と点との距離は外積を使って

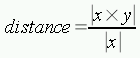
distance = |x×y| / |x|

で求まります（ここで |x×y| は実数に対する絶対値， |x| はベクトルに対する絶対値と「絶対値」の意味が異なっている点に注意してください）。 コーディングは以下の通りです*1：

// 点a,bを通る直線と点cとの距離
double distance_l_p(P a, P b, P c) {
  return abs(cross(b-a, c-a)) / abs(b-a);
}

線分と点の距離

今度は線分と点の距離を考えてみましょう。 距離としてどのような値が欲しいのか，というのは問題依存なのですが， ここでは一般的な距離の定義に従って，点から「線分のどこか」への最短距離としてみます。 そうすると，線分 ab に垂直な直線で点 a を通る直線と点 b を通る直線に囲まれた領域（下図の左の赤色領域に相当）にある点であれば， 点から直線 ab への垂線が最短距離になります。 また，点 c がこの赤色の領域の外であれば，点 c が a 側なら最短距離は2点 a, c の距離と等しく， 点 c が b 側なら最短距離は2点 b, c の距離と等しくなることが分かります。

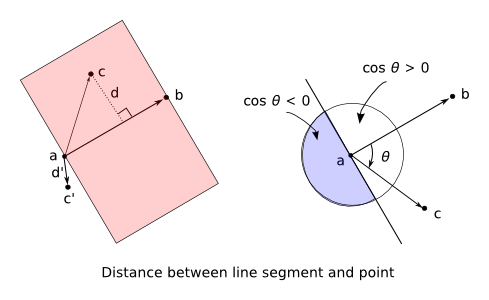
点 c が a より内か外かを調べるには，前回の「点が線分上にあるかないか」の判定で用いた内積を利用した方法が使えます。 すなわち，ベクトル x = b - a と ベクトル y = c - a のcosが負であれば a の外側ということが分かるので， その場合は点 c と点 a との距離を最短距離とします（上図の右）。 b 側についても同様です。

コーディングは以下の通りです：

// 点a,bを端点とする線分と点cとの距離
double distance_ls_p(P a, P b, P c) {
  if ( dot(b-a, c-a) < EPS ) return abs(c-a);
  if ( dot(a-b, c-b) < EPS ) return abs(c-b);
  return abs(cross(b-a, c-a)) / abs(b-a);
}

ここでは比較に EPS を使わずに 0.0 を用いても構わない（計算結果の距離はせいぜい計算誤差の範囲内になる）のですが， このようにEPSを使って垂線上の点も含めた方がこの関数の計算全体がより早く終了します。

線分の交差判定

次に2線分が交差しているかどうかを考えます。

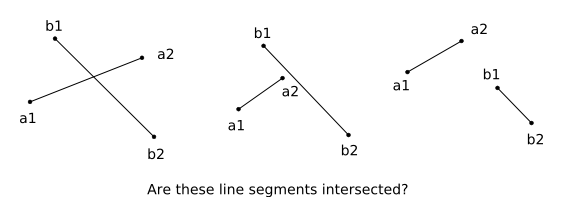
線分 a = a2 - a1 と線分 b = b2 - b1 が交差している場合，線分 b の端点 b1 と b2 は必ず線分 a の両側にあります。 また，線分 a の端点 a1 と a2 は必ず線分 b の両側にあります（上図の左）。 逆に交差していない場合，線分 a か線分 b のどちらかから見て，両点ともに片側にある場合が必ずあるといえます。 上図の中央の例の場合，線分 a から見れば b1, b2 は線分 a の両側にありますが，線分 b から見れば a1, a2 は両方とも線分 b の右側にあります。 これは交差していれば当然のことといえます。

ある点が線分（ベクトル）の左側にあるか右側にあるかというのは，外積を使えば判定できます（下図）。

sinは0度～180度で正の値，180度～360度で負の値を取るので，点がベクトルの左側なら外積は正，右側なら外積は負になります。 従って，もし端点が両側にあるなら正と負，片側にあるなら正と正もしくは負と負になるので， 2つの外積の値を掛けて正になれば非交差ということが分かります。 また，線分 a と線分 b の両方について，相手線分の両端点との外積の値の積が負になれば交差ということが分かります。

以上より，2線分の交差判定のプログラムは次のようになります （外積の積が0であれば線上に点があることになりますが，これは交差しているとみなしています）：

// a1,a2を端点とする線分とb1,b2を端点とする線分の交差判定
int is_intersected_ls(P a1, P a2, P b1, P b2) {
  return ( cross(a2-a1, b1-a1) * cross(a2-a1, b2-a1) < EPS ) &&
         ( cross(b2-b1, a1-b1) * cross(b2-b1, a2-b1) < EPS );
}

線分の交点計算

次に，交差しているならばその交点を求めてみましょう。

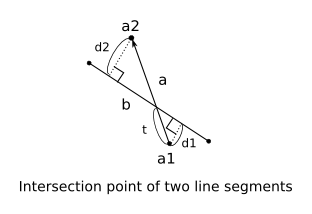
上図より，線分 a の始点 a1 からのパラメータ t を求めれば，交点 p は

p = a1 + at

で求めることができます。

パラメータ t は，点 a1 から直線 b の距離 d1 と点 a2 から直線bの距離 d2 との比 (t:1-t = d1:d2) から，

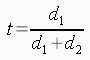
t = d1 / (d1 + d2)

で計算できます。 点と直線の距離は前述の通りで，外積を用いて求めます。

以上より，2線分の交点を求めるプログラムは次のようになります（前提：2線分は交差している）：

// a1,a2を端点とする線分とb1,b2を端点とする線分の交点計算
P intersection_ls(P a1, P a2, P b1, P b2) {
  P b = b2-b1;
  double d1 = abs(cross(b, a1-b1));
  double d2 = abs(cross(b, a2-b1));
  double t = d1 / (d1 + d2);

  return a1 + (a2-a1) * t;
}

距離を求めるときに |b| で割っていないのは，d1 / (d1 + d2) で結局打ち消されるからです。

なお，このプログラムは a1, a2 を端点とする線分と b1, b2 を通る直線の交点を求めることもできます（先に交差判定が必要です）。

直線の交点計算

最後に直線の交点計算を考えます。 まず，2直線は平行でなければ必ず交差しており，交点を持ちます。 平行判定は外積の性質である

a×b = 0 ⇔ a//b

を使用すればOKです。 一応プログラムで書けば

// a1,a2を通る直線とb1,b2を通る直線の交差判定
int is_intersected_l(P a1, P a2, P b1, P b2) {
  return !EQ( cross(a1-a2, b1-b2), 0.0 );
}

となりますが，平行時の例外処理は問題依存です。 以降は，平行でない（＝どこかで交わっている）という前提で話をします。

さて，点 a1, a2 を通る直線と点 b1, b2 を通る直線の交点を求めるのですが，ここで提示する基本的な戦略は

  1. ベクトル b = b2 - b1 は直線として扱う
  2. ベクトル a = a2 - a1 を伸び縮みさせて，交点まで到達するベクトルを作る（結果，そのベクトルは交点座標を持つ）

ことです。

ベクトル b は直線として扱うので1通り（向きはありますが）に対して，ベクトル a は下図の3通りが考えられます。

まず直線 b に垂直な軸を考えて，その軸上で上図に示す d1, d2 の長さを求めます。 この直線 b とその法線が成す直交座標系における d1:d2 の比は， 元の座標系における「目的のベクトル:元々のベクトルa」の比と同じになります（目的のベクトルは a1 を始点，交点を終点とするベクトル）。 従って，交点を指す位置ベクトルは

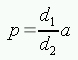
p = (d1 / d2) a

で求めることができます。

言い換えると，ベクトル a の大きさを d2 で割って正規化し，それを長さ d1 倍するとも考えられます。 正規化するための係数 d2 は，上図より

d2 = b×a

で求めることができます。 また，長さを表す係数 d1 は

d1 = b×(b1 - a1)

で求めることができます。

なお，係数 d1 および d2 の正負は検証しておく必要があるでしょう。 d1 に関しては，左・中央の図では正，右の図では負になり，正常に動作しそうです（外積の正負に関しては「線分の交差判定」の図を参照）。 d2 に関しては，上図では全て正となるのでOKです。 図を上下反転させる，すなわち a = a2 - a1 ではなく a = a1 - a2 ととった場合や， 図の左右反転，すなわち b = b1 - b2 とする場合でも，d1 および d2 は期待通りです。

以上より，次のプログラムが導かれます（前提：2直線は平行でない）：

// a1,a2を通る直線とb1,b2を通る直線の交点計算
P intersection_l(P a1, P a2, P b1, P b2) {
  P a = a2 - a1; P b = b2 - b1;
  return a1 + a * cross(b, b1-a1) / cross(b, a);
}

線分の交点計算は上図の中央のケースですから，当然このアルゴリズムは線分の交点計算でも使用できます。 また，線分の交差判定についても，このアルゴリズムでとりあえず交点を計算してみて，その交点が両線分上にあるかどうかで判定できます。

補足1: ここではC++を前提としているので実数の絶対値を取るのにabsを使っています。 Cではabsの替わりにfabsを使ってください。 C++ではabsはdouble型に対してもオーバーロードされているので問題ありませんが， Cではabsはint型に対してのみ有効なので気をつけてください。

$Id: lines.shtml 1282 2007-02-03 09:05:17Z SYSTEM $