数値計算の結果をプロットする(2)
のこぎり波は次のような形状をしています。
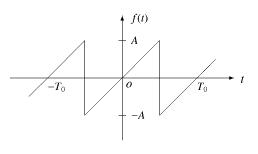
この周期波形のフーリエ級数を求めると,
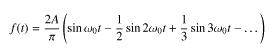
となります。なお,
![]()
であり,f0を基本周波数と呼びます。 ここで,tが変数で,A, f0が定数になります。 また,計算を有限時間で終了させるために,第n次高調波(第n項のsinの値)まで求めることにし, nを定数として宣言しておくことにします。
ここでは A = 1, f0 = 1[kHz], -2[ms] <= t <= 2[ms], dt = 0.01[ms] としてプログラムを書いてみましょう。
以下がそのプログラムです。
/* Numeral Computing with gnuplot: 2 */
#include <stdio.h>
#include <math.h>
#define N 10 /* 第N高調波までを計算 */
#define A 1.0 /* 振幅 */
#define F 1e3 /* 基本周波数 f0 [Hz] */
#define T_DIV 100e3 /* サンプリング周波数(1秒間当たりのtの分割数) [Hz] */
#define T_START -2e-3 /* tの最小値 [s] */
#define T_END 2e-3 /* tの最大値 [s] */
int main(void);
int main(void) {
int i; /* ステップ数 */
int j; /* 高調波を求めるループの制御変数 */
double t; /* ステップiにおける時刻t */
double y; /* f(t) */
int sign; /* 各項の符号 */
double k, omega; /* 計算量を減らすために,定数項をあらかじめ計算しておく */
double pi; /* π (= 3.14...) */
pi = 4 * atan(1.0);
k = 2 * A / pi;
omega = 2 * pi * F;
for (i=T_START*T_DIV; i<=T_END*T_DIV; i++) {
t = (double)i / T_DIV;
y = 0;
sign = 1;
for (j=1; j<=N; j++) {
y += sign * sin(j * omega * t) / j;
sign *= -1; /* 符号を反転 */
}
y = k * y;
printf("%f %f\n", t, y);
}
return 0;
}
このCソースコードをコンパイルして,実行結果をnc2.pltに出力します。 なお,math.hをインクルードしているのでコンパイル時には-lmオプションをつける必要があります。
% gcc -o nc2 nc2.c -lm % ./nc2 > nc2.plt
そしてgnuplotでプロットします。
# 結果 gnuplot> plot 'nc2.plt' w l
Nの値を変更して,実行結果のグラフがどう変化するかを調べてみてください。
$Id: numeric_computing2.shtml 1289 2007-02-04 13:22:39Z SYSTEM $