数値計算の結果をプロットする(3)

数値計算の結果をプロットする(1)で計算した関数

f(x) = (x^3)/2 - x^2 + 20*x

を差分方程式で表して解いてみましょう(差分方程式って何？って方はこちら)。 まず，この関数の増減を調べるために両辺を微分すると，次のようになります。

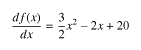
df(x)/dx = (3/2)*x^2 - 2x + 20

これはxにおける曲線 f(x) の増減（正確には傾き）を表した方程式ですが， 1次微分が含まれている方程式なのでこれを1階の微分方程式と呼びます。

次に，この微分方程式を前進オイラー法で差分方程式に変換します。 微分の定義より，lim dx->0 を極小な値のdxで近似して，

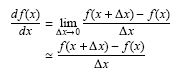
df(x)/dx ~= {f(x+dx) - f(x)} / dx

この式を元の式に代入すると，

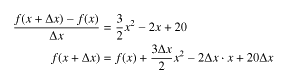
f(x + dx) = f(x) + {(3*dx)/2}*x^2 - 2*dx*x + 20*dx

となります。 現在のxからdx進んだ f(x) の値（左辺）が，現在のf(x)の値＋その点からの増減（右辺）で表されています。 これが f(x) の差分方程式です。

では前々回と同じように，xの範囲を -10 <= x < 10，dxを0.1としてプログラムを作ってみましょう。

nc3.c

/* Numeral Computing with gnuplot: 3 */

#include <stdio.h>

int main(void);

int main(void) {
  int n;            /* ステップ数 */
  double x;         /* ステップ n における x の値 */
  double y;         /* x における y の値 */
  double dx = 0.1;  /* ステップ毎のxの増減*/

  /* 最初の値 f(-10) を求める */
  x = -10.0;
  y = (x*x*x)/2 - x*x + 20*x;
  printf("%f %f\n", x, y);
  for (n=1; n<=200; n++) {
    y = y + (3*dx*x*x)/2 - 2*dx*x + 20*dx;
    x = x + dx;
    printf("%f %f\n", x, y);
  }

  return 0;
}

このCソースコードをコンパイルして，実行結果をnc3.pltに出力します。

% cc -o nc3 nc3.c
% ./nc3 > nc3.plt

そしてgnuplotでプロットします。

# 結果

gnuplot> plot 'nc3.plt' w l, 'nc1.plt' w l  # nc1.pltも同時にプロット

nc1.pltとは値が少しずれていることが分かります。 dxを変更して，値のずれがどう変化するかを調べてみてください。

$Id: numeric_computing3.shtml 1289 2007-02-04 13:22:39Z SYSTEM $